SMIR Generator
Abstract
A method is proposed for simulating the sound pressure signals on a spherical microphone array in a reverberant enclosure. The method employs spherical harmonic decomposition (SHD) and takes into account scattering from a solid sphere. An analysis shows that the error in the decomposition can be made arbitrarily small given a sufficient number of spherical harmonics.
- D. P. Jarrett, E. A. P. Habets, M. R. P. Thomas and P. A. Naylor, "Rigid sphere room impulse response simulation: algorithm and applications," Journal of the Acoustical Society of America, Volume 132, Issue 3, pp. 1462-1472, 2012.
- D. P. Jarrett, E. A. P. Habets, M. R. P. Thomas and P. A. Naylor, "Simulating room impulse responses for spherical microphone arrays," Proc. of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2011), Prague, Czech Republic, May 22-27, 2011.
- J.B. Allen and D.A. Berkley, "Image method for efficiently simulating small-room acoustics," Journal Acoustic Society of America, 65(4), April 1979, p 943.
Example
procFs = 8000; % Sampling frequency (Hz)
c = 343; % Sound velocity (m/s)
nsample = 512; % Length of desired RIR
N_harm = 40; % Maximum order of harmonics to use in SHD
K = 2; % Oversampling factor
L = [4 6 8]; % Room dimensions (x,y,z) in m
sphLocation = [2 3.2 4]; % Receiver location (x,y,z) in m
s = [2.37 4.05 4.4]; % Source location(s) (x,y,z) in m
beta = [1 0.7 0.7 0.5 0.2 1]; % Room reflection coefficients [\beta_x_1
% \beta_x_2 \beta_y_1 \beta_y_2 \beta_z_1 \beta_z_2]
order = -1; % Reflection order (-1 is maximum reflection order)
sphRadius = 0.042; % Radius of the sphere (m)
sphType = 'rigid'; % Type of sphere (open/rigid)
mic = [pi/4 pi; pi/2 pi]; % Microphone positions (azimuth, elevation)
[h, H, beta_hat] = smir_generator(c, procFs, sphLocation, s, L, beta, sphType, sphRadius,
mic, N_harm, nsample, K, order);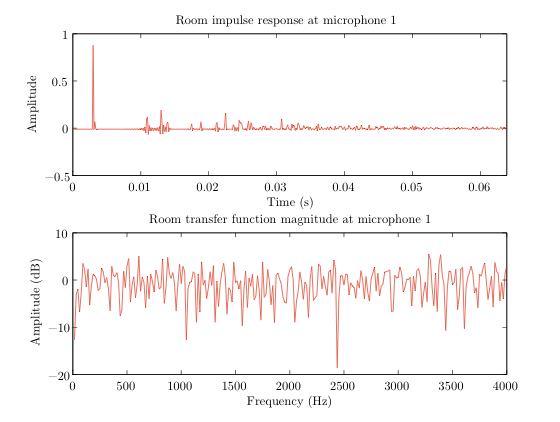
History
| 1.0.20101017 (DJ) | Initial version |
| 1.1.20111212 (DJ) | Performance improvements, added C++ function function (with MEX wrapper) for most computationally complex operations, added reflection order limit |
| 1.2.20120925 (DJ) | Added truncation of time domain RIRs when oversampling (K > 1) is used | 2.0.20130830 (SB) |
Implemented main loop in C++ Added source directivity Added angle dependent reflection coefficient |
2.1.20150713 (SB) |
Fixed default RIR length computation |
(JD) Daniel Jarrett
(SD) Sebastian Braun
Download
Notes
- The most computationally complex parts of this algorithm have been placed in a C++ function with a MEX wrapper. To use it you will need to build the MEX-function using MATLAB's mex command.
- Spherical coordinate system:
- The functions mysph2cart() and mycart2sph() are included in order to convert between spherical and Cartesian coordinates. These functions use the same coordinate system as the Eigenmike.
- The microphone angles used as inputs to the SMIR generator must be obtained using mycart2sph(), or use the same coordinate system. Specifically, azimuth is measured counterclockwise from the positive x axis (the positive y axis has an azimuth of 90°) and inclination is measured from the positive z axis (the x-y plane has an inclination of 90°).
- Oversampling: When the source-array distance is short, it is necessary to oversample in the frequency domain in order to avoid the wrap-around effect of the discrete Fourier transform. For this purpose, choose K > 1, e.g., K = 2 or K = 4.
- The example script run_smir_generator_comparison compares the output of the SMIR generator to the output of Dr Emanuel Habets's RIR generator, with each of the array's microphones treated as a separate receiver. This comparison is only valid in the open sphere case, since the RIR generator does not account for scattering. A copy of the RIR generator is included for this purpose, in accordance with the terms of the GNU General Public License. To use it you will need to build the MEX-function using MATLAB's mex command.
- Because of the reciprocity principle, we can use SMIRgen to generate an impulse response from a source on a sphere (simulating a mouth) to an omnidirectional receiver.

