dYIN and dSWIPE: Differentiable Variants of Classical Fundamental Frequency Estimators
Sebastian Strahl, Meinard Müller
This website is related to the following article:
- Sebastian Strahl and Meinard Müller
dYIN and dSWIPE: Differentiable Variants of Classical Fundamental Frequency Estimators
IEEE/ACM Transactions on Audio, Speech, and Language Processing, 33: 2622–2633, 2025. PDF Details Code DOI@article{StrahlM25_df0_TASLP, author = {Sebastian Strahl and Meinard M{\"u}ller}, title = {{dYIN} and {dSWIPE}: {D}ifferentiable Variants of Classical Fundamental Frequency Estimators}, journal = {{IEEE/ACM} Transactions on Audio, Speech, and Language Processing}, volume = {33}, pages = {2622--2633}, year = {2025}, doi = {10.1109/TASLPRO.2025.3581119} url-pdf = {https://audiolabs-erlangen.de/content/05_fau/professor/00_mueller/03_publications/2025_StrahlM_df0_TASLP_ePrint.pdf}, url-details = {https://audiolabs-erlangen.de/resources/MIR/2025-TASLPRO-dYIN-dSWIPE}, url-code = {https://github.com/groupmm/df0}, }
Abstract
Fundamental frequency (F0) estimation is a critical task in audio, speech, and music processing applications, such as speech analysis and melody extraction. F0 estimation algorithms generally fall into two paradigms: classical signal processing-based methods and neural network-based approaches. Classical methods, like YIN and SWIPE, rely on explicit signal models, offering interpretability and computational efficiency, but their non-differentiable components hinder integration into deep learning pipelines. Neural network-based methods, such as CREPE, are fully differentiable and flexible but often lack interpretability and require substantial computational resources. In this paper, we propose differentiable variants of two classical algorithms, dYIN and dSWIPE, which combine the strengths of both paradigms. These variants enable gradient-based optimization while preserving the efficiency and interpretability of the original methods. Through several case studies, we demonstrate their potential: First, we use gradient descent to reverse-engineer audio signals, showing that dYIN and dSWIPE produce smoother gradients compared to CREPE. Second, we design a two-stage vocal melody extraction pipeline that integrates music source separation with a differentiable F0 estimator, providing an interpretable intermediate representation. Finally, we optimize dSWIPE's spectral templates for timbre-specific F0 estimation on violin recordings, demonstrating its enhanced adaptability over SWIPE. These case studies highlight that dYIN and dSWIPE successfully combine the flexibility of neural network-based methods with the interpretability and efficiency of classical algorithms, making them valuable tools for building end-to-end trainable and transparent systems.
dYIN

Visualization of the dYIN algorithm. The cumulative mean normalized difference function (CMNDF) is computed for each frame, with the vertical axis of $\mathbf D^\text{(t)}$ representing time lag and the horizontal axis representing time. The time lag axis is then converted into a frequency axis ($\mathbf D^\mathrm{(f)}$), and framewise application of the softmin function converts the values into probabilities, resulting in an F0 salience matrix $\hat{\mathbf{Y}}_\mathrm{dYIN}$. If needed, F0 selection approaches can process the probabilistic output into scalar F0 estimates.
dSWIPE
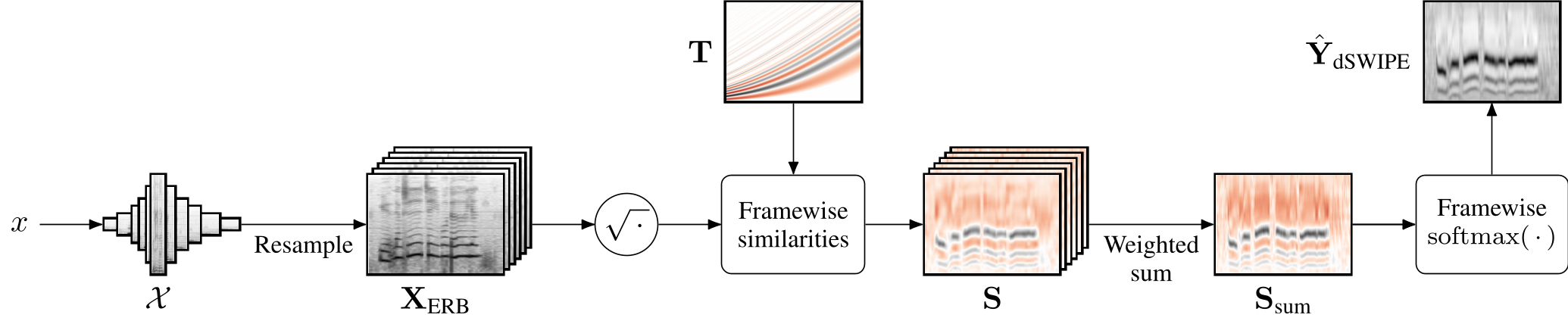
Visualization of the dSWIPE algorithm. Spectral representations are extracted from the audio signal ($\mathcal X$) and aligned on a common time and frequency axis ($\mathbf{X}_\text{ERB}$). These are then compared with predefined spectral templates for different F0 classes ($\mathbf T$) to compute similarity scores ($\mathbf S$). The similarity scores are aggregated ($\mathbf S_\mathrm{sum}$) and normalized to produce an F0 salience matrix ($\hat{\mathbf Y}_\text{dSWIPE}$). Red is used to visualize negative values
Case Study 1: Reverse Engineering
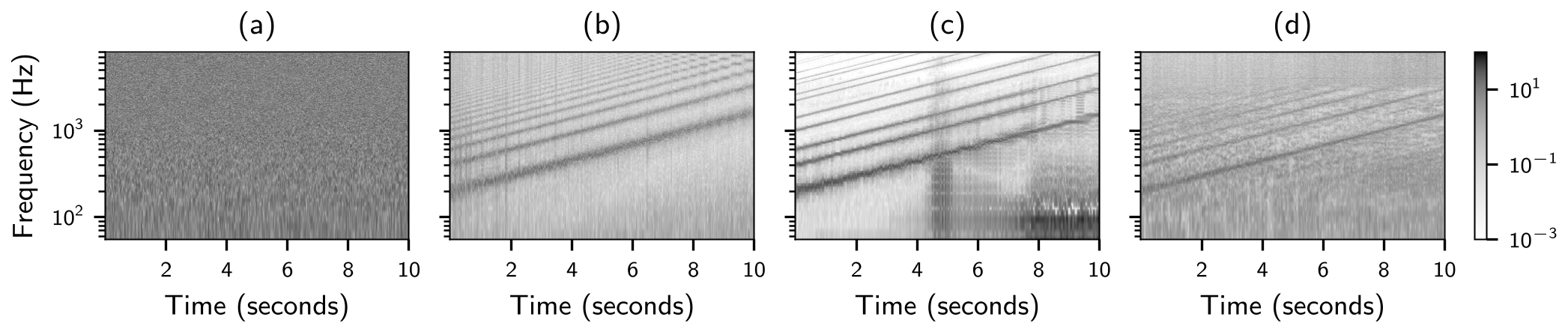
In this experiment, we explore the input signal required by each F0 estimator to produce a user-specified F0 trajectory. To find such signals, we create an initial signal $x^\text{(init)}$ consisting of random noise, which serves as the starting point for optimization. We do not assume any signal model, but each sample of the signal is treated as an independent parameter to be optimized. Additionally, we define a target F0 trajectory that increases exponentially in frequency from 200 Hz to 1500 Hz over a duration of 10 seconds, representing the F0 contour of a chirp-like signal. For each F0 estimator, starting with $x^\text{(init)}$ as input, we iteratively compute the classification loss between the estimator's predictions and the target vectors and apply gradient descent with respect to the samples of the time-domain input signal. Below, all signals are illustrated using spectrograms.
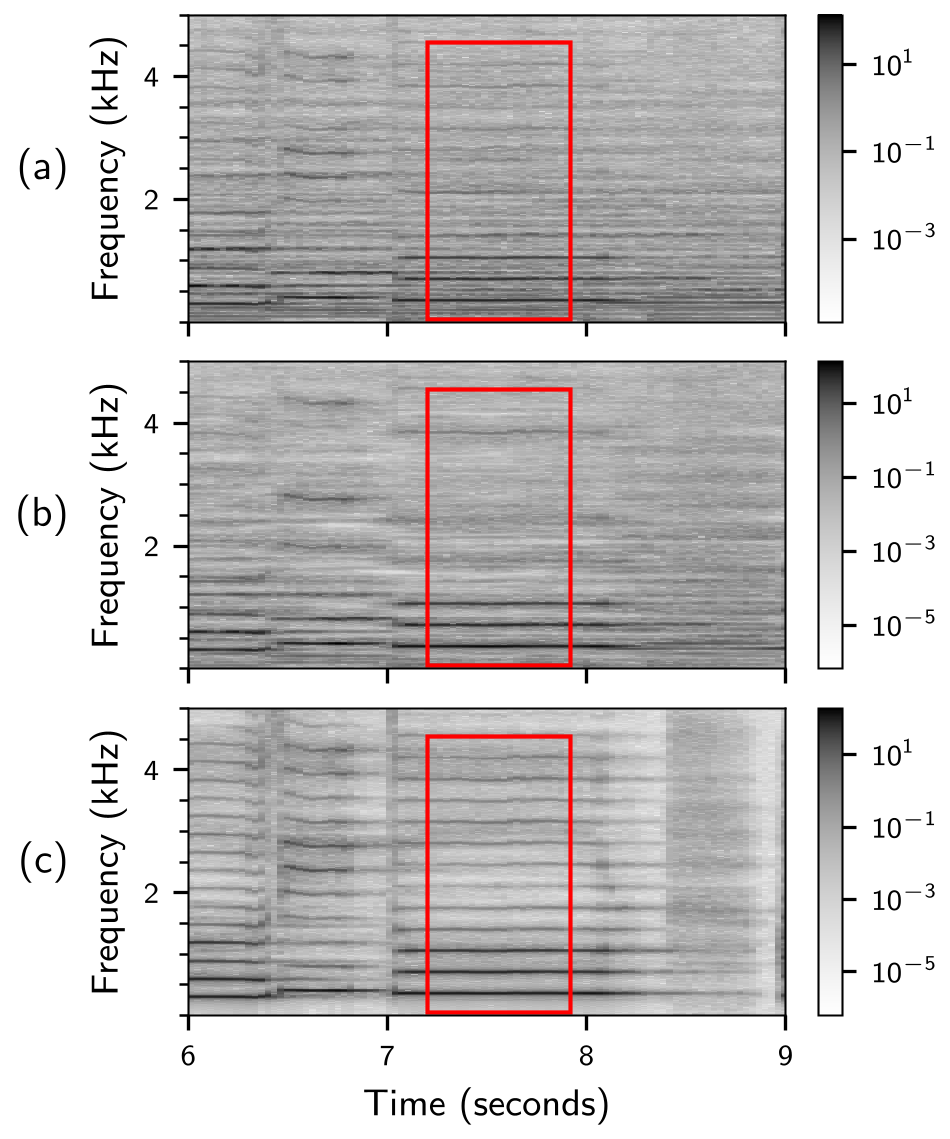
Case Study 2: Vocal Melody Extraction
In this second case study, we address vocal melody extraction which involves estimating the F0 trajectory of a monophonic singing voice within a polyphonic music context [5]. We use a two-step approach, consisting of a vocal melody separator (VMS) and an F0 estimator. With the output of the VMS, our pipeline provides an intermediate source separation-like representation. For a detailed description, we refer to our article.
Below, we show spectrograms of a mixture signal and intermediate representations for different pipelines.
Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Grant No. 500643750 (MU 2686/15-1). The authors are with the International Audio Laboratories Erlangen, a joint institution of the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) and Fraunhofer Institute for Integrated Circuits IIS.
References
- Alain de Cheveign 'e and Hideki Kawahara
YIN, a fundamental frequency estimator for speech and music.
Journal of the Acoustical Society of America (JASA), 111(4): 1917–1930, 2002.@article{CheveigneK02_YIN_JASA, author = {Alain de Cheveign{\'e} and Hideki Kawahara}, title = {{YIN}, a fundamental frequency estimator for speech and music.}, journal = {Journal of the Acoustical Society of America (JASA)}, year = {2002}, volume = {111}, pages = {1917--1930}, number = {4}, } - Arturo Camacho and John G. Harris
A sawtooth waveform inspired pitch estimator for speech and music
The Journal of the Acoustical Society of America, 124(3): 1638–1652, 2008.@article{CamachoH08_SawtoothWaveform_JASA, author = {Arturo Camacho and John G. Harris}, title = {A sawtooth waveform inspired pitch estimator for speech and music}, publisher = {ASA}, year = {2008}, journal = {The Journal of the Acoustical Society of America}, volume = {124}, number = {3}, pages = {1638--1652}, } - Jong Wook Kim, Justin Salamon, Peter Li, and Juan Pablo Bello
CREPE: A Convolutional Representation for Pitch Estimation
In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP): 161–165, 2018. DOI@inproceedings{KimSLB18_CREPE_ICASSP, author = {Jong Wook Kim and Justin Salamon and Peter Li and Juan Pablo Bello}, title = {{CREPE}: {A} Convolutional Representation for Pitch Estimation}, booktitle = {Proceedings of the {IEEE} International Conference on Acoustics, Speech and Signal Processing ({ICASSP})}, address = {Calgary, Canada}, pages = {161--165}, year = {2018}, doi = {10.1109/ICASSP.2018.8461329} } - Chao-Ling Hsu and Jyh-Shing Roger Jang
On the Improvement of Singing Voice Separation for Monaural Recordings Using the MIR-1K Dataset
IEEE Transactions on Audio, Speech, and Language Processing, 18(2): 310–319, 2010.@article{HsuJang10_SingingVoiceSeparationUnvoiced_IEEE-TASLP, author = {Chao-Ling Hsu and Jyh-Shing Roger Jang}, journal = {{IEEE} Transactions on Audio, Speech, and Language Processing}, title = {On the Improvement of Singing Voice Separation for Monaural Recordings Using the {MIR-1K} Dataset}, year = {2010}, month = {February}, volume = {18}, number = {2}, pages = {310--319}, } - Justin Salamon, Emilia Gómez, Daniel P. W. Ellis, and Gaël Richard
Melody Extraction from Polyphonic Music Signals: Approaches, applications, and challenges
IEEE Signal Processing Magazine, 31(2): 118–134, 2014. DOI@article{SalamonGER14_MelodyTracking_IEEE-SPM, author = {Justin Salamon and Emilia G{\'o}mez and Daniel P. W. Ellis and Ga{\"e}l Richard}, title = {Melody Extraction from Polyphonic Music Signals: {A}pproaches, applications, and challenges}, journal = {{IEEE} Signal Processing Magazine}, volume = {31}, number = {2}, pages = {118--134}, year = {2014}, doi = {10.1109/MSP.2013.2271648}, timestamp = {Tue, 24 Jun 2014 19:06:27 +0200}, biburl = {http://dblp.uni-trier.de/rec/bib/journals/spm/SalamonGER14}, bibsource = {dblp computer science bibliography, http://dblp.org} }

