Background information

Our objective was to modify (initially by filtering) audio signals coded with by an MPEG-1/2 audio coder without having to decompress them first. In other words, we were comparing filtering in the compressed domain to the process of decoding the compressed signal, filtering it in the time domain, and re-encoding the signal for further transmission or re-storage. The idea was to modify such a compressed signal and still leave it as a compressed signal. The reason for doing this was to save operations.

During our initial work, we noticed that some filters, such as lowpass filters, could simply be run through the MPEG-1/2 polyphase filter bank to obtain 32 subfilters, and then each subfilter could be applied to the appropriate subband of the compressed signal to give us the desired perceptual effect without causing distortion.

However, more complicated filters, such as multiband bandpass filters or filters corresponding to head-related transfer functions, cause more complex modifications to the frequency components of the audio signal. Using the simple MPEG-1 polyphase filter bank decomposition with these complicated filters gave us some semblance of the desired frequency-domain result, but very audible aliasing was also created.

The solution was to build a set of filters which operate on the spectral values delivered by the polyphase filterbank out of the desired time-domain filters using a matrix-based analysis of the polyphase filter bank. The basic idea, without getting bogged down in too much detail, is as follows.

Suppose we represent our time-domain filter by the convolution matrix C, the MPEG analysis filter bank by H, and the polyphase synthesis filter bank by G. If our audio signal is denoted by x, then simple encoding is represented by

x' = Hx.

Decoding is then given by

y = GHx.

If we do filtering on the decoded signal, we get

y' = CGHx.

To do filtering in the compressed domain, we must access the signal x', so we get

x'' = C'x' = C'Hx,

where C' is a subband-domain version of C. How do we calculate it? Well, first, we have our objective:

GC'Hx = CGHx.

That is, we want the subband-domain filtered signal, when decoded, to be perceptually equivalent to the signal that was first decoded and then filtered in the time domain. If we solve this equation for C', we get

C' = G-1CG,

which can be approximated (pretty closely since G ~= H-1) by

C' ~= HCG.

This subband-domain version of C (given above by C') can then be applied in the polyphase domain to obtain the desired perceptual effect without introducing aliasing distortion.

This technique can be extended in a relatively straightforward manner to build matrices and filters for polyphase-domain sampling rate conversion as well. For details, please refer to the references at the end of this page.

Sound examples

Two items have been filtered using the following processing techniques:

• Bandpass-filter applied in the compressed domain
• Bandpass filter applied in the time domain
• Bandpass filter applied by scaling the individual subband samples
• Sampling rate conversion from 44.1 kHz to 32 kHz in the time domain
• Sampling rate conversion from 44.1 kHz to 32 kHz in the compressed domain

Play Female Voice

Original

Play Female Voice_MPEG-BPF

Bandpass filtered in the compressed domain

Play Female Voice TD-BPF

Bandpass filtered in the time domain

Play Female Voice scaling BPF

Bandpass filtered using subband scaling

Play Female Voice TD-SRC

Sampling rate conversion in the time domain

Play Female Voice MPEG-SRC

Sampling rate conversion in the compressed domain

Play Gilmour

Original

Play Gilmour_MPEG-BPF

Bandpass filtered in the compressed domain

Play Gilmour TD-BPF

Bandpass filtered in the time domain

Play Gilmour scaling BPF

Bandpass filtered using subband scaling

Play Gilmour TD-SRC

Sampling rate conversion in the time domain

Play Gilmour MPEG-SRC

Sampling rate conversion in the compressed domain

Additionally, the bandpass filter used for the analysis is included. This filter was applied directly in the time domain, and was used as the prototype filter to generate the compressed-domain filters.

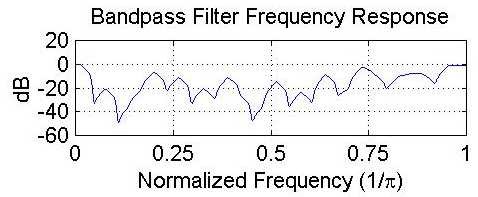
References

Lanciani, Christopher A., Compressed-Domain Processing of MPEG Audio Signals, PhD Thesis, Georgia Institute of Technology, 1999.
Lanciani, Christopher A. and Ronald W. Schafer, "Psychoacoustically-based Processing of MPEG-I Layer 1-2 Encoded Signals," presented at the IEEE Signal Processing Society 1997 Workshop on Multimedia Signal Processing, June 23-25, 1997, Princeton, NJ.
Lanciani, Christopher A. and Ronald W. Schafer, "Subband-domain Filtering of MPEG Audio Signals," presented at the IEEE International Conference on Acoustics, Speech, and Signal Processing, March 15-19, 1999, Phoenix, AZ.
Lanciani, Christopher A. and Ronald W. Schafer, "Application of Head-related Transfer Functions to MPEG Audio Signals," presented at the 31st Symposium on System Theory, March 21-23, 1999, Auburn, AL.

Note: Some of the audio source excerpts have been taken from the SQAM CD [Cat. No. 422204-2] by kind permission of the European Broadcasting Union (EBU)