Following Section 5.1.2 of [Müller, FMP, Springer 2015], we introduce in this notebook some basic facts on musical scales and the circle of fifths.
Introduction¶
Besides intervals and chords, we now consider another important musical construct that is referred to as a musical scale. Again, adopting a rather simplistic view, a scale can be regarded as a set of notes, where the elements are typically ordered by ascending pitch. While a chord may be thought of as a vertical structure, a scale is usually associated to horizontal structures. Assuming the principle of octave equivalence, scales typically span a single octave, with higher or lower octaves simply repeating the pattern. In this way, a musical scale can be regarded as a division of the octave space into a certain number of scale steps, where each scale step is an interval between two successive notes.
Chromatic Scale¶
As first example, we consider the twelve-tone equal-tempered scale, where an octave is subdivided into twelve scale steps. This scale is also referred to as chromatic scale. In this case, all scale steps correspond to the same interval having a size of one semitone (or $100$ cents). Due to enharmonic equivalence, there are various spellings and score notations to represent a chromatic scale. Two of them are shown in the following figure. Furthermore, we provide a piano recording as well as a synthesized version of the chromatic scale (generated in the next code cell).

import numpy as np
import IPython.display as ipd
def generate_sinusoid_scale(pitches=[69], duration=0.5, Fs=4000, amplitude_max=0.5):
"""Generate synthetic sound of scale using sinusoids
Notebook: C5/C5S1_Scales_CircleFifth.ipynb
Args:
pitches (list): List of pitchs (MIDI note numbers) (Default value = [69])
duration (float): Duration (seconds) (Default value = 0.5)
Fs (scalar): Sampling rate (Default value = 4000)
amplitude_max (float): Amplitude (Default value = 0.5)
Returns:
x (np.ndarray): Synthesized signal
"""
N = int(duration * Fs)
t = np.arange(0, N) / Fs
x = []
for p in pitches:
omega = 2 ** ((p - 69) / 12) * 440
x = np.append(x, np.sin(2 * np.pi * omega * t))
x = amplitude_max * x / np.max(x)
return x
duration = 0.25
Fs = 4000
pitches = [60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72]
x = generate_sinusoid_scale(pitches=pitches, duration=duration, Fs=Fs)
print('Chromatic scale', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))
Major and Minor Scale¶
In the following, we only consider scales that are subsets of the chromatic scale, where the scale steps can be specified in semitones. In the context of scales, the minor second (one semitone) is also referred to as a half step and the major second (two semitones) as a whole step. As with chords, there are two scale types that are of particular importance in Western music theory. The first scale type is known as a major scale, which is made up of seven notes and a repeated octave. The first note of a major scale is called the key note of the scale. Starting with the key note, the sequence of intervals between the successive notes of a major scale is as follows (using C4 as key note):

The chroma name of the key note also determines the name of the scale. For example, the major scale starting with a $\mathrm{C}$ is called the $\mathrm{C}$-major scale. Sometimes, the bold character $\mathbf{C}$ (as used for chords) is also used as an abbreviation to refer to the scale. The other major scales are then obtained by cyclically shifting the $\mathrm{C}$-major scale. The notes of a major scale are given names, also known as scale degrees, to specify their positions relative to the key note. The key note is also called the tonic, which is the main note of the scale. The fourth note of the scale is called the subdominant and the fifth note the dominant. The remaining names are indicated in the following figure:

The second scale type we consider is known as the (natural) minor scale. Similar to a major scale, a minor scale consists of seven notes and a repeated octave. This time, however, the sequence of intervals between the notes is as follows (using C4 as key note):
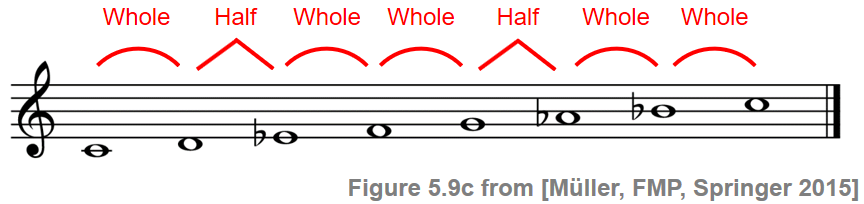
Again, there are twelve minor scales with naming conventions similar to those of the minor chords. Both major and minor scales can be subsumed under the general term diatonic scale, which is (by definition) a seven-pitch scale with five whole steps and two half steps for each octave, where the two half steps are separated from each other by either two or three whole steps.
In the following code cell, we generate a synthesized version of the $\mathrm{C}$-major scale and $\mathrm{C}$-minor scale, respectively.
duration = 0.5
x_maj = generate_sinusoid_scale(pitches=[60, 62, 64, 65, 67, 69, 71, 72], duration=duration, Fs=Fs)
x_min = generate_sinusoid_scale(pitches=[60, 62, 63, 65, 67, 68, 70, 72], duration=duration, Fs=Fs)
print('C-major scale', flush=True)
ipd.display(ipd.Audio(data=x_maj, rate=Fs))
print('C-minor scale (natural)', flush=True)
ipd.display(ipd.Audio(data=x_min, rate=Fs))
Further Scales¶
There are many more scales used in Western music and beyond. For example, besides the minor scale introduced above (also referred to as the natural minor scale), there are other types of minor scales called the harmonic minor and melodic minor scale. The notes of the harmonic minor scale are the same as the natural minor except that the seventh degree is raised by one semitone, resulting in an augmented second between the sixth and seventh degrees. We have already mentioned the chromatic scale, which involves twelve pitches. There are other scales such as the pentatonic scale consisting of five pitches, the whole tone scale consisting of six pitches, or the octatonic scale (diminished scale) consisting of eight pitches. In the following code cell, we generate synthesized versions of these scales.
Harmonic minor scale (7 pitches + octave):

Pentatonic scale (5 pitches + octave):

Whole tone scale (6 pitches + octave):
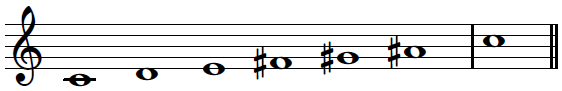
Octatonic scale (8 pitches + octave):
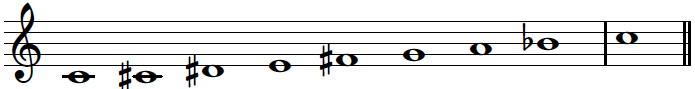
duration = 0.5
x_mh = generate_sinusoid_scale(pitches=[60, 62, 63, 65, 67, 68, 71, 72], duration=duration, Fs=Fs)
x_p = generate_sinusoid_scale(pitches=[60, 62, 64, 67, 69, 72], duration=duration, Fs=Fs)
x_w = generate_sinusoid_scale(pitches=[60, 62, 64, 66, 68, 70, 72], duration=duration, Fs=Fs)
x_o = generate_sinusoid_scale(pitches=[60, 61, 63, 64, 66, 67, 69, 70, 72], duration=duration, Fs=Fs)
print('Harmonic minor scale (7 pitches + octave)', flush=True)
ipd.display(ipd.Audio(data=x_mh, rate=Fs))
print('Pentatonic scale (5 pitches + octave)', flush=True)
ipd.display(ipd.Audio(data=x_p, rate=Fs))
print('Whole tone scale (6 pitches + octave)', flush=True)
ipd.display(ipd.Audio(data=x_w, rate=Fs))
print('Octatonic scale (8 pitches + octave)', flush=True)
ipd.display(ipd.Audio(data=x_o, rate=Fs))
Circle of Fifths¶
One characteristic property of diatonic scales is that they can be obtained from a chain of six successive perfect fifth intervals. For example, the $\mathrm{C}$-major scale is obtained from an ascending chain of six perfect fifths starting with $\mathrm{F}$:
\begin{equation} \mathrm{F}-\mathrm{C}-\mathrm{G}-\mathrm{D}-\mathrm{A}-\mathrm{E}-\mathrm{B}. \end{equation}Being the most consonant non-octave interval, the fifth interval plays a particularly important role when relating notes, chords, and scales. All notes being related by fifths gives a diatonic scale a degree of coherence and balance. Furthermore, these fifth relationships also make it possible to relate entire musical scales. This leads us to the famous circle of fifths, which is a visual representation of the relationships among the twelve tones of the chromatic scale and the associated major and minor scales. Intuitively, the circle of fifths reflects the degree of "musical" similarity between different scales—the closer two scales are located on the circle, the more they share in terms of tonal material.
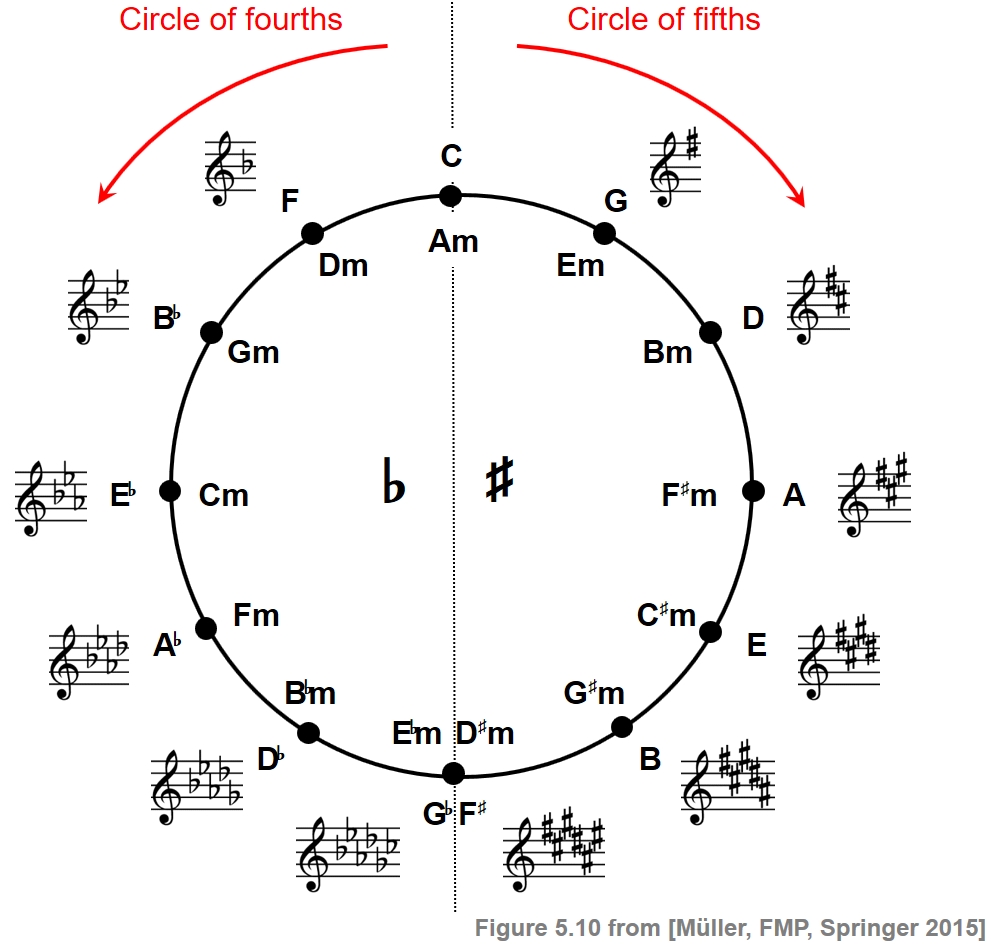
In the following recording, the tonic (key note) of each scale is played going around the circle of fifths in a clockwise fashion:
\begin{equation} \mathrm{C}-\mathrm{G}-\mathrm{D}-\mathrm{A}-\mathrm{E}-\mathrm{B}-\mathrm{G}^\flat-\mathrm{D}^\flat-\mathrm{A}^\flat-\mathrm{E}^\flat-\mathrm{B}^\flat-\mathrm{F} \end{equation}Musical Keys¶
More formally, the circle of fifths represents the relations between musical keys—a concept that is closely connected to major and minor scales. While a scale is an ordered set of notes typically used in a key, the key is the center of gravity, established by particular chord progressions. At the top of the circle of fifths, there is the $\mathrm{C}$-major key. The notes of the corresponding $\mathrm{C}$-major scale, which correspond to the white keys of a piano keyboard, do not require any accidental ($\sharp$, $\flat$) when encoded in Western music notation. As a result, the key signature of $\mathrm{C}$ major has no flats or sharps. The $\mathrm{A}$-minor key, whose corresponding scale consists of the same seven notes, shares the same key signature with $\mathrm{C}$-major. In general, for each major key there is a minor key whose corresponding scales share the same notes. This relationship is referred to as a relative relationship. In the circle of fifths shown above, the major keys are noted outside the circle, whereas the corresponding relative minor keys are noted inside the circle.
Starting with the $\mathrm{C}$-major key at the top of the circle, one obtains the other keys proceeding in a clockwise fashion by ascending fifths. The next key is the $\mathrm{G}$-major key, whose corresponding scale shares six notes with the $\mathrm{C}$-major scale; only the $\mathrm{F}$ in $\mathrm{C}$ major becomes an $\mathrm{F}^\sharp$ in $\mathrm{G}$ major. This introduces a sharp in the key signature for $\mathrm{G}$ major. The same kind of relations hold between any two subsequent keys or scales along the circle of fifths. Proceeding one fifth upwards changes one note of the scale and introduces one additional sharp in the key signature. Repeating this process twelve times in the equal-tempered case, one returns to the original $\mathrm{C}$-major, thus closing the circle (when assuming enharmonic equivalence).
Similarly, one can travel along the circle in a counterclockwise fashion by descending fifths, which corresponds to ascending fourths. Proceeding in a circle of fourths introduces an additional flat in the resulting key signature.
In the following table, we provide a synthesized version of all $24$ major and minor scales ordered along the circle of fifth.
import pandas as pd
from collections import OrderedDict
duration = 0.25
scale_major = np.array([60, 62, 64, 65, 67, 69, 71, 72])
scale_minor = np.array([57, 59, 60, 62, 64, 65, 67, 69])
scale_major_name = ['C','G','D','A','E','B','F$^\sharp$',
'D$^\\flat$','A$^\\flat$','E$^\\flat$','B$^\\flat$','F','C',]
scale_minor_name = ['Am','Em','Bm','F$^\sharp$m','C$^\sharp$m','G$^\sharp$m','D$^\sharp$m',
'B$^\\flat$m','Fm','Cm','Gm','Dm','Am',]
scale_major_list = []
for i in range(13):
x = generate_sinusoid_scale(pitches=scale_major, duration=duration, Fs=Fs)
scale_major_list.append(x)
scale_major += 7
if scale_major[-1] > 80:
scale_major -= 12
scale_minor_list = []
for i in range(13):
x = generate_sinusoid_scale(pitches=scale_minor, duration=duration, Fs=Fs)
scale_minor_list.append(x)
scale_minor += 7
if scale_minor[-1] > 80:
scale_minor -= 12
audio_tag_html_list_major = []
for i in range(13):
audio_tag = ipd.Audio(scale_major_list[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: 200px; height: 30px;"')
audio_tag_html_list_major.append(audio_tag_html)
audio_tag_html_list_minor = []
for i in range(13):
audio_tag = ipd.Audio(scale_minor_list[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: 200px; height: 30px;"')
audio_tag_html_list_minor.append(audio_tag_html)
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('Major', scale_major_name),
(' ', audio_tag_html_list_major),
('Minor', scale_minor_name),
(' ', audio_tag_html_list_minor)]))
#df.index = np.arange(0, len(df))
#df = df.T
ipd.HTML(df.to_html(escape=False, justify='center', index=True, header=True))










