Following Section 1.3.2 of [Müller, FMP, Springer 2015], we cover in this notebook the relation between frequency and pitch.
Sinusoids¶
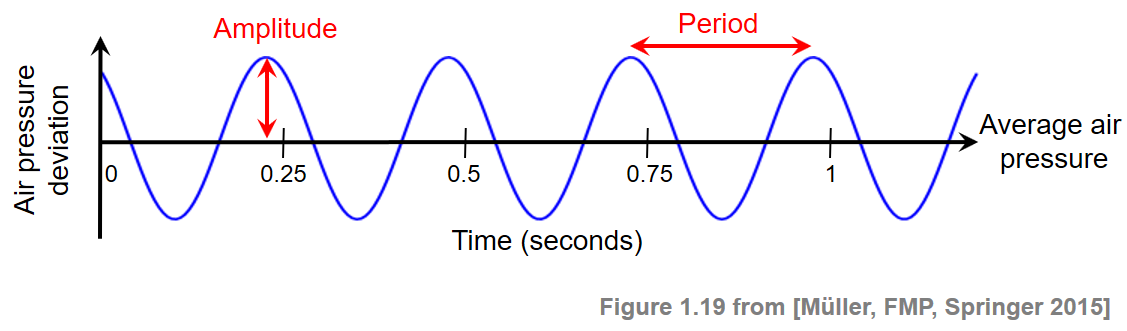
A sound wave can be visually represented by a waveform. If the points of high and low air pressure repeat in an alternating and regular fashion, the resulting waveform is called periodic. In this case, the period of the wave is defined as the time required to complete a cycle. The frequency, measured in Hertz (Hz), is the reciprocal of the period. The simplest type of periodic waveform is a sinusoid, which is completely specified by its frequency, its amplitude (the peak deviation of the sinusoid from its mean), and its phase (determining where in its cycle the sinusoid is at time zero). The following figure shows a sinusoid with frequency $4~\mathrm{Hz}$.
Audible Frequency Range¶
The higher the frequency of a sinusoidal wave, the higher it sounds. The audible frequency range for humans is between about $20~\mathrm{Hz}$ and $20000~\mathrm{Hz}$ ($20~\mathrm{kHz}$). Other species have different hearing ranges. For example, the top end of a dog's hearing range is about $45~\mathrm{kHz}$, a cat's is $64~\mathrm{kHz}$, while bats can even detect frequencies beyond $100~\mathrm{kHz}$. This is why one can use a dog whistle, which emits ultrasonic sound beyond the human hearing capability, to train and to command animals without disturbing nearby people.
In the following experiment, we generate a chirp signal which frequency increases by a factor of two (one octave) every second. Starting with $80~\mathrm{Hz}$, the frequency raises to $20480~\mathrm{Hz}$ over a total duration of $8$ seconds.
import IPython.display as ipd
import numpy as np
import sys
sys.path.append('..')
import libfmp.c1
Fs = 44100
dur = 1
freq_start = 80 * 2**np.arange(8)
for f in freq_start:
if f==freq_start[0]:
chirp, t = libfmp.c1.generate_chirp_exp_octave(freq_start=f, dur=dur, Fs=Fs, amp=1)
else:
chirp_oct, t = libfmp.c1.generate_chirp_exp_octave(freq_start=f, dur=dur, Fs=Fs, amp=1)
chirp = np.concatenate((chirp, chirp_oct))
ipd.display(ipd.Audio(chirp, rate=Fs))
Similarly, we generate a chirp signal starting with $640~\mathrm{Hz}$ and going down $20~\mathrm{Hz}$ over a total duration of $10$ seconds.
Fs = 8000
dur = 2
freq_start = 20 * 2**np.arange(5)
for f in freq_start:
if f==freq_start[0]:
chirp, t = libfmp.c1.generate_chirp_exp_octave(freq_start=f, dur=dur, Fs=Fs, amp=1)
else:
chirp_oct, t = libfmp.c1.generate_chirp_exp_octave(freq_start=f, dur=dur, Fs=Fs, amp=1)
chirp = np.concatenate((chirp,chirp_oct))
chirp = chirp[::-1]
ipd.display(ipd.Audio(chirp, rate=Fs))
Pitches and Center Frequencies¶
The sinusoid can be considered the prototype of an acoustic realization of a musical note. Sometimes the sound resulting from a sinusoid is called a harmonic sound or pure tone. The notion of frequency is closely related to what determines the pitch of a sound. In general, pitch is a subjective attribute of sound. In the case of complex sound mixtures its relation to frequency can be especially ambiguous. In the case of pure tones, however, the relation between frequency and pitch is clear. For example, a sinusoid having a frequency of $440~\mathrm{Hz}$ corresponds to the pitch $\mathrm{A4}$. This particular pitch is known as concert pitch, and it is used as the reference pitch to which a group of musical instruments are tuned for a performance. Since a slight change in frequency does not necessarily lead to a perceived change, one usually associates an entire range of frequencies with a single pitch.
Two frequencies are perceived as similar if they differ by a power of two, which has motivated the notion of an octave. For example, the perceived distance between the pitches $\mathrm{A3}$ ($220~\mathrm{Hz}$) and $\mathrm{A4}$ ($440~\mathrm{Hz}$ is the same as the perceived distance between the pitches $\mathrm{A4}$ and $\mathrm{A5}$ ($880~\mathrm{Hz}$). In other words, the human perception of pitch is logarithmic in nature. This perceptual property has already been used to define the equal-tempered scale that subdivides an octave into twelve semitones based on a logarithmic frequency axis. More formally, using the MIDI note numbers, we can associate to each pitch $p\in[0:127]$ a center frequency $F_\mathrm{pitch}(p)$ (measured in Hz) defined as follows:
$$ F_\mathrm{pitch}(p) = 2^{(p-69)/12} \cdot 440. $$The MIDI note number $p=69$ serves as reference and corresponds to the pitch $\mathrm{A4}$ ($\mathrm{440~Hz}$). Increasing the pitch number by $12$ (an octave) leads to an increase by a factor of two. The following figure shows a portion of a piano keyboard with the keys labeled by the pitch names and the MIDI note numbers.

Using the formula for $F_\mathrm{pitch}$, we compute in the next code cell the center frequencies for all MIDI pitch $p\in[21:108]$ corresponding to the notes of a standard piano keyboard (A0 to C8).
def f_pitch(p):
"""Compute center frequency for (single or array of) MIDI note numbers
Notebook: C1/C1S3_FrequencyPitch.ipynb
Args:
p (float or np.ndarray): MIDI note numbers
Returns:
freq_center (float or np.ndarray): Center frequency
"""
freq_center = 2 ** ((p - 69) / 12) * 440
return freq_center
chroma = ['A ', 'A#', 'B ', 'C ', 'C#', 'D ', 'D#', 'E ', 'F ', 'F#', 'G ', 'G#']
for p in range(21, 109):
print('p = %3d (%2s%1d), freq = %7.2f ' % (p, chroma[(p-69) % 12], (p//12-1), f_pitch(p)))
From this formula, it follows that the frequency ratio of two subsequent pitches $p+1$ and $p$ is constant:
$$ F_\mathrm{pitch}(p+1)/F_\mathrm{pitch}(p) = 2^{1/12} \approx 1.059463 $$Generalizing the notion of semitones, the cent denotes a logarithmic unit of measure used for musical intervals. By definition, an octave is divided into $1200$ cents, so that each semitone corresponds to $100$ cents. The difference in cents between two frequencies, say $\omega_1$ and $\omega_2$, is given by
$$ \log_2\left(\frac{\omega_1}{\omega_2}\right)\cdot 1200. $$The interval of one cent is much too small to be heard between successive notes. The threshold of what is perceptible, also called the just noticeable difference, varies from person to person and depends on other aspects such as the timbre and the musical context. As a rule of thumb, normal adults are able to recognize pitch differences as small as $25$ cents very reliably, with differences of $10$ cents being recognizable only by trained listeners. As in illustration, we generate a sinusoid of $440~\mathrm{Hz}$ used as reference and further sinusoids with various differences.
def difference_cents(freq_1, freq_2):
"""Difference between two frequency values specified in cents
Notebook: C1/C1S3_FrequencyPitch.ipynb
Args:
freq_1 (float): First frequency
freq_2 (float): Second frequency
Returns:
delta (float): Difference in cents
"""
delta = np.log2(freq_1 / freq_2) * 1200
return delta
def generate_sinusoid(dur=5, Fs=1000, amp=1, freq=1, phase=0):
"""Generation of sinusoid
Notebook: C1/C1S3_FrequencyPitch.ipynb
Args:
dur (float): Duration (in seconds) (Default value = 5)
Fs (scalar): Sampling rate (Default value = 1000)
amp (float): Amplitude of sinusoid (Default value = 1)
freq (float): Frequency of sinusoid (Default value = 1)
phase (float): Phase of sinusoid (Default value = 0)
Returns:
x (np.ndarray): Signal
t (np.ndarray): Time axis (in seconds)
"""
num_samples = int(Fs * dur)
t = np.arange(num_samples) / Fs
x = amp * np.sin(2*np.pi*(freq*t-phase))
return x, t
dur = 5
Fs = 4000
pitch = 69
ref = f_pitch(pitch)
freq_list = ref + np.array([0,2,5,10,ref])
for freq in freq_list:
x, t = generate_sinusoid(dur=dur, Fs=Fs, freq=freq)
print('freq = %0.1f Hz (MIDI note number 69 + %0.2f cents)' % (freq, difference_cents(freq,ref)))
ipd.display(ipd.Audio(data=x, rate=Fs))










