Following Section 5.1.2 of [Müller, FMP, Springer 2015], we introduce in this notebook some basic facts on musical chords.
Introduction¶
Intuitively, a chord can be loosely defined as a group of several notes that sound simultaneously. While most researchers agree that a chord should contain at least three notes, others also regard a combination of two notes as a chord. Depending on the number of distinct notes contained in a chord, one also speaks of a dyad (two notes, corresponding to intervals), a triad (three notes), a tetrad (four notes), and so on. In harmony analysis, notes that are one or several octaves apart are often considered to belong to the same "sound quality." Therefore, when defining the concept of a chord, it may be more precise to speak of distinct pitch classes rather than of distinct notes.
Triads¶
Despite being an oversimplification, we restrict our considerations in the following to a small selection of chords. In Western music, the most important triads consist of three notes that can be stacked in thirds. When stacked in thirds, the lowest note is referred to as the root note. Since there are minor thirds (three semitones) and major thirds (four semitones), one can distinguish between four types of such triads: major triad, minor triad, diminished triad, and augmented triad. The following figure illustrates these types of triads over the root note C4.

Each of the chord types can be played based on different root notes. Regardless of the given root note, the four triad types have a different quality in how they are perceived by a listener. Consisting of a major third and a perfect fifth, the major triads comprise consonant intervals. Furthermore, there is a high agreement among the partials of the three constituent notes. As a result, the sound of a major triad is often described as being coherent, pleasant, and happy. By reducing the pitch of the second note by one semitone, a major triad transforms into a minor triad. Still regarded as consonant and coherent, minor chords are often perceived as sad, gloomy, or somber. For the diminished and augmented triads, there is little overlap in the partials of the constituent notes, and these triads are typically perceived as dissonant and unstable. Often, diminished and augmented triads are used in transitional passages to move between more stable harmonies based on major and minor chords.
In the following, we present a sound example of a $\mathrm{C}$-major and $\mathrm{C}$-minor chord played on a piano (as shown in the above figure). We then generate a synthetic variant of each of the four chord types using sinusoids.
Major triad:
Minor triad:
import numpy as np
import IPython.display as ipd
def generate_sinusoid_chord(pitches=[69], duration=1, Fs=4000, amplitude_max=0.5):
"""Generate synthetic sound of chord using sinusoids
Notebook: C5/C5S1_Chords.ipynb
Args:
pitches (list): List of pitches (MIDI note numbers) (Default value = [69])
duration (float): Duration (seconds) (Default value = 1)
Fs (scalar): Sampling rate (Default value = 4000)
amplitude_max (float): Amplitude (Default value = 0.5)
Returns:
x (np.ndarray): Synthesized signal
"""
N = int(duration * Fs)
t = np.arange(0, N) / Fs
x = np.zeros(N)
for p in pitches:
omega = 2 ** ((p - 69) / 12) * 440
x = x + np.sin(2 * np.pi * omega * t)
x = amplitude_max * x / np.max(x)
return x
duration = 2
Fs = 4000
pitches = [60, 64, 67]
x = generate_sinusoid_chord(pitches=pitches, duration=duration, Fs=Fs)
print('Major chord', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))
pitches = [60, 63, 67]
x = generate_sinusoid_chord(pitches=pitches, duration=duration, Fs=Fs)
print('Minor chord', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))
pitches = [60, 63, 66]
x = generate_sinusoid_chord(pitches=pitches, duration=duration, Fs=Fs)
print('Diminished chord', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))
pitches = [60, 64, 68]
x = generate_sinusoid_chord(pitches=pitches, duration=duration, Fs=Fs)
print('Augmented chord', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))
Major and Minor Chords¶
Since there are twelve different root notes (up to enharmonic equivalence and octave shifts), one can basically form twelve major and twelve minor triads. In the following, we show a score representation of these triads, where the lowest note of each chord is the root note. Furthermore, we provide a piano recording as well as a synthesized version of each of triads.


duration = 1
Fs = 4000
x_major = []
pitches = np.array([60, 64, 67])
for i in range(12):
x = generate_sinusoid_chord(pitches=pitches+i, duration=duration, Fs=Fs)
x_major = np.append(x_major, x)
x_minor = []
pitches = np.array([60, 63, 67])
for i in range(12):
x = generate_sinusoid_chord(pitches=pitches+i, duration=duration, Fs=Fs)
x_minor = np.append(x_minor, x)
print('Major chords', flush=True)
ipd.display(ipd.Audio(data=x_major, rate=Fs))
print('Minor chords', flush=True)
ipd.display(ipd.Audio(data=x_minor, rate=Fs))
On the note level, there are generally many alternatives for realizing a given chord. When a chord's lowest note (the bass note) is its root, the chord is said to be in root position or in normal form. When the root is not the lowest note played in a chord, it is said to be inverted. The following figure shows some variants of the $\mathrm{C}$-major chord including the normal form, the first inversion, the second inversion, a chord with octave doublings, and a broken chord (where the notes of a chord may be played one after the other).

Fs = 4000
duration = 2
x = []
x = generate_sinusoid_chord(pitches=[60, 64, 67], duration=duration, Fs=Fs)
x = np.append(x,generate_sinusoid_chord(pitches=[64, 67, 72], duration=duration, Fs=Fs))
x = np.append(x,generate_sinusoid_chord(pitches=[67, 72, 76], duration=duration, Fs=Fs))
x = np.append(x,generate_sinusoid_chord(pitches=[60, 64, 67, 72, 76], duration=duration, Fs=Fs))
duration = duration / 8
broken_chord = [60, 64, 67, 72, 76, 67, 72, 76]
for p in broken_chord:
x = np.append(x,generate_sinusoid_chord(pitches=[p], duration=duration, Fs=Fs))
ipd.display(ipd.Audio(data=x, rate=Fs))
A major chord is usually denoted with the same symbol as used for the pitch class of its root note. In the following, we use bold characters to distinguish the concept of a chord from the concept of a pitch class or note. For the minor chords, one often uses the same notation as for major chords except for adding a letter $\mathbf{m}$ that refers to "minor." For example, the $\mathrm{C}$-major chord denoted by $\mathbf{C}$ consists of the three notes with pitch classes $\mathrm{C}$, $\mathrm{E}$, and $\mathrm{G}$, while the $\mathrm{C}$-minor chord denoted by $\mathbf{Cm}$ consists $\mathrm{C}$, $\mathrm{E}^\flat$, and $\mathrm{G}$.
Mathematical Model¶
Adopting a rather simplistic view, where a major or minor chord is determined by the pitch classes or chroma values of its constituent notes, one can regard each of the triads as a three-element subset of the set $\{\mathrm{C},\mathrm{C}^\sharp,\mathrm{D},\ldots\mathrm{B}\}$ that consists of the twelve chroma attributes. Equivalently, a three-element subset can be regarded as a binary chroma vector with three entries of value $1$ at the chroma positions encoded by the subset. Based on this mathematical model, the twelve major chords can be obtained by cyclically shifting the major triad $\mathbf{C}$ in twelve different ways. Similarly, one obtains the twelve minor chords from $\mathbf{Cm}$. Note that each of the $24$ major and minor triads lead to a different three-element subset. In other words, on the pitch-class level, the major and minor chords are uniquely defined. The resulting chroma patterns of the $24$ major and minor chords are shown in the following figure:
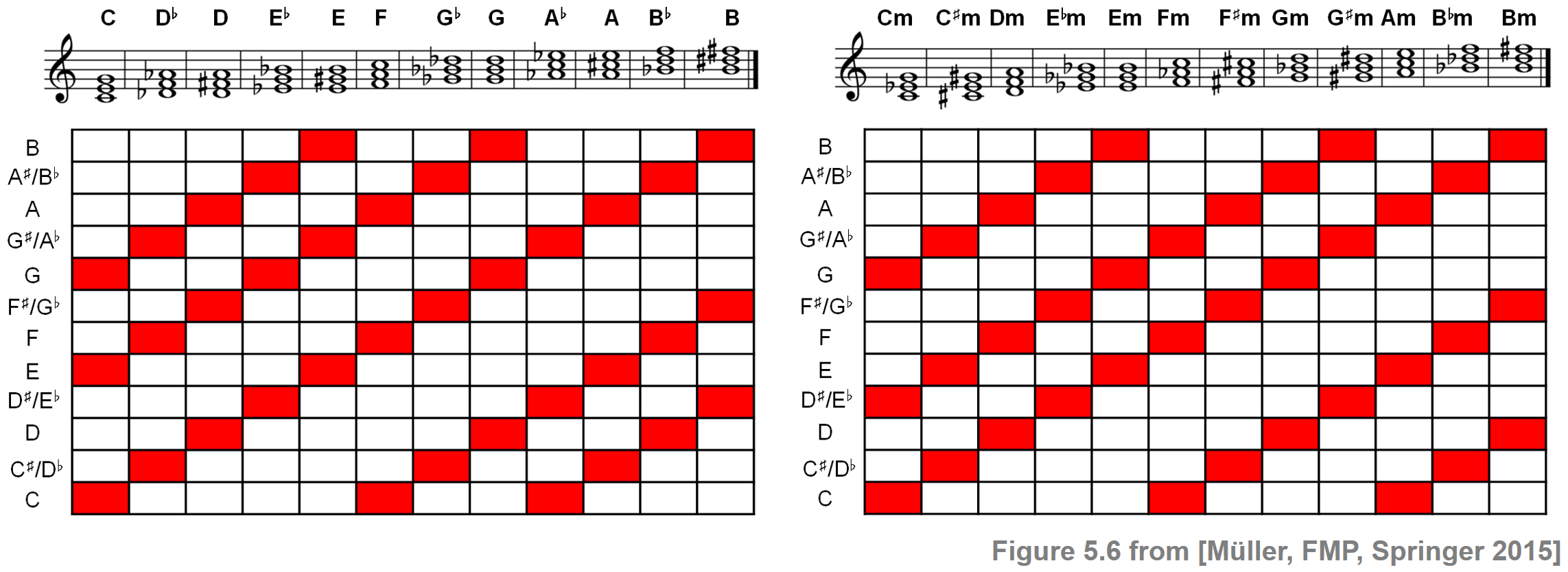
In the FMP notbook on template-based chord recognition, we will provide an implementation to generate the binary chroma vectors underlying these patterns.
Seventh Chords and Beyond¶
The triads also appear as subsets of more complex chords consisting of four, five or even more notes. Stacking one further third interval onto a triad leads to a seventh chord. There are many possible types of seventh chords. The major seventh chord is obtained by stacking a major third onto a major triad and is mainly used in pop and jazz music. Well-known is the dominant seventh chord (major triad + minor third), which has a strong tendency to resolve to the next chord. The minor seventh chord (minor triad + minor third) is more stable and appears both in pop/rock/jazz and in classical music. The half-diminished seventh chord (diminished triad + major third) is used extensively in Romantic music (e.g., by Richard Wagner) as well as in jazz music. Finally, the diminished seventh chord (diminished triad + minor third), consisting of three concatenated minor thirds, is used for modulations to different keys already in Baroque music. More information can be found in the literature on music theory.











