Online dereverberation for dynamic scenarios using a Kalman filter with an autoregressive model
S. Braun and E. A. P. Habets
Published in the IEEE Signal Processing Letters, 2016.
Abstract
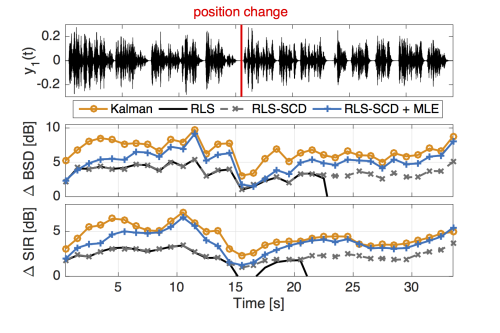
Reverberant signals can be modeled in the short-time Fourier transform (STFT) domain using a frequency dependent autoregressive (AR) model. In state-of-the-art, these AR coefficients have been considered stationary, which does not hold in time-varying environments. We propose to model these AR coefficients using a first-order Markov process, whereas the reverberant microphone signal observations are considered deterministic. This leads to a framework where the AR coefficients can be optimally estimated using a Kalman filter per subband. As a consequence, we can dereverberate the observed signals by applying the estimated AR coefficients as an adaptive linear filter per subband. Estimators for the required statistical parameters in the Kalman filter are derived. Due to the adaptive solution, the algorithm is suitable for real-time applications. It is shown that the proposed method outperforms an existing recursive least squares solution in terms of reverberation reduction, convergence time and tracking changes in the acoustic scene.
Audio Examples
- The signals are obtained using measured impulse responses with 2 microphones in a room with 630 ms reverberation time. There are two speakers sequentially speaking at two different positions.
- The original RLS uses a spectral subtraction rule to estimate the speech variance, which additionally requires the reverberation time. By using the RLS with the ML our proposed covariance estimator, the performance can be significantly improved.